Earnshaw's Theorem, or: Why Frogs Can Float, but Magnets Won't
When thinking about trapping of magnetic particles such as atoms, we often say that particles that seek out strong magnetic fields (bar magnets, compass needles) cannot be trapped with stationary fields. Referred to as Earnshaw’s theorem, it’s usually encountered as its restatement that ‘Magnetic field maxima are forbidden!’ Samuel Earnshaw, however, wasn’t in the business of messing around with magnets in his shed, no, he had greater ambitions. He was trying to figure out what type of particle could make up the aether (the medium which was at the time held responsible for conveying light) by putting bounds on the forces that could exist between them. Here he is, arguing that no potential $V$ derived from a force that falls off with the distance as $1/r^2$ can hold a particle in place by putting other particles at fixed positions [1]:
Since at least one of the quantities $\partial^2 V/\partial x^2$, $\partial^2 V/\partial y^2$, $\partial^2 V/\partial z^2$, is negative, and at least one positive, there will be at least one principal axis parallel to which a disturbed particle can vibrate, and at least one parallel to which a disturbed particle cannot vibrate.1
It’s an interesting result, and Earnshaw uses it to argue that the aether could instead be held together by forces falling off as $1/r^n$ where $n < 2$. While we don’t remember him for putting a dent in the aether theory of light, his result does have profound consequences for the trapping of particles using electromagnetic fields. It’s quite easy to see, for instance, why a charged particle can never be stably held by a static electric field in free space. Mathematically, this means that the potential cannot have a local minimum. Since the force $\vec{F}$ on a charge $q$ in an electric field $\vec{E}$ satisfies $\vec{F} = q\vec{E} = -\nabla V$, this can be confirmed with Gauss’s law, which states that the electric field is divergence-free in the absence of charges, or $\nabla \cdot \vec{E} = 0$. From this we have $\nabla^2 V = -q \nabla \cdot \vec{E} = 0$, which means that - by the second derivative test - $V$ can only contain saddle points.2
Fortunately, this doesn’t imply that it is fundamentally impossible to trap charged particles, it just means it cannot be done without any moving parts. People who trap ions, for instance, have developed several types of traps using rapidly oscillating electric fields. The Paul trap, for instance, looks like a rotating saddle:
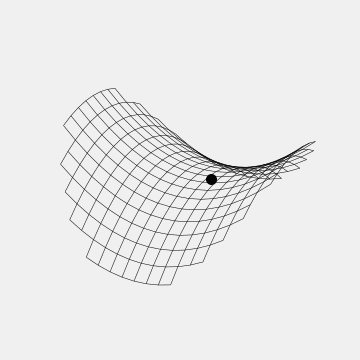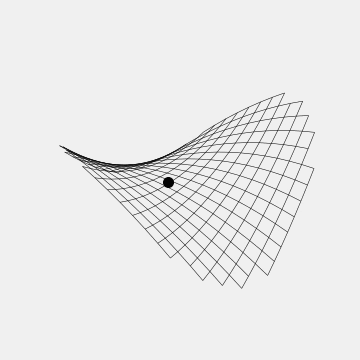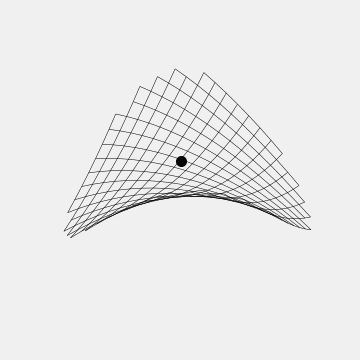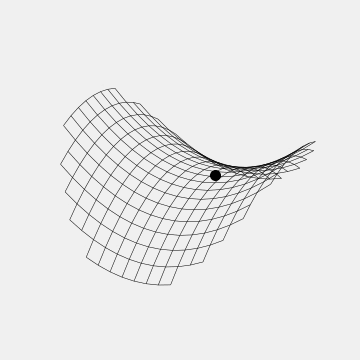
It’s not immediately obvious why this line of reasoning would apply to the magnetic interaction though, and indeed the result is a bit more subtle, but it’s also more permissive. Specifically, it turns out it is possible to construct static magnetic traps, for instance for atoms and yes, frogs.
The complication is that the fundamental magnetic interaction we’re usually concerned with is that between a dipole and a field. A dipole, unlike a point charge, has an orientation, and so the interaction energy includes a dot product: $U = -\vec{\mu}\cdot\vec{B}$. As the compass needle shows us, permanent magnets tend to orient themselves to point along the any external magnetic field; $\vec{\mu}$ points in the same direction as $\vec{B}$, and so $U$ is minimized. The same holds for materials that can be magnetized because they contain iron, such as the door of your fridge: a magnet will induce a dipole moment $\mu \propto B$ in the door, also pointing in the same direction as $B$. (Because of this we call the door of your fridge a paramagnet.)
In both cases, the energy depends on the magnitude of the magnetic field: $U \propto -|\vec{B}|$, and so to figure out whether there are maxima, minima, or saddle points we need to take the second derivative of a quantity related to the field: $\nabla^2 U$. Using Maxwell’s equations it’s possible to show3 that $\nabla^2 U \leq 0$, from which it follows that $U$ can only have local maxima and saddle points, meaning it’s impossible to design a static magnetic field that traps a dipole $\mu$.
Not so fast, though. It turns out a lot of materials have an opposite (albeit small) response to external magnetic fields; these materials - called diamagnets - develop a magnetization that points in a direction opposite to that of the external field, and so $U = -\vec{\mu}\cdot\vec{B} \propto \left| \vec{B} \right|$. But this turns the entire argument on its head! All the signs flip, which now means $U$ can have local minima.
Diamagnetism is weak, though, so it’s difficult to actually levitate everyday objects using it. An exception is formed by magnets levitating above superconducting materials, but the frog that was famously levitated by Andre Geim proves the point: it required a magnetic field of 16 T. This is so strong it can be considered an achievement of its own!
These constraints also have some implications for trapping neutral atoms. Most atoms have a nonzero magnetic dipole moment, which either arises from the atoms’ constituents (the protons, neutrons, and electrons, all possessing some intrinsic dipole), or the orbits of the electrons around the core. Because of additional interactions between these dipoles and their alignment with respect to each other, it depends on the atom its internal state whether it prefers to seek out a magnetic field minimum or maximum. (In the latter case it wouldn’t be trappable, for the same reason paramagnets aren’t.) Fortunately, for a large number of species it’s possible to transfer the atoms in some state that is trappable.
All of this is not quite what Earnshaw was talking about when he was deliberating on the stuff that held the vacuum together. Calling these results “Earnshaw, but for magnets,” may therefore be a little inaccurate, especially because it is possible to trap magnetic dipoles with static field; the only requirement is that their response has the right sign. Some people instead choose to refer to it as Wing’s theorem [3,4], although it is not clear who proved it first [2].
Bibliography
Footnotes
1 By ‘vibrate’ he meant that a potential is confining along a particular axis, and can hence support some oscillatory motion. ‘Cannot vibrate’ is a euphemism for ‘gets kicked out.’
2 This argument is actually a little more subtle, and I’ll give but a hand-waving explanation here. If the first derivative of $V$ is zero at some point $\vec{x}$, this point is a saddle point if the eigenvalues of the Hessian matrix are both positive and negative. If we do a basis transformation such that the Hessian is diagonal, the eigenvalues are on the diagonal. Summing them, we get $\nabla^2 V$, which we know must be zero. Except for the case where all eigenvalues are zero, we must have some mixture of positive and negative values.
3 The proof (see e.g. Ref. [2]) feels distinctly more complicated than for the electric counterpart of the theory. It’s a bit more straightforward to carry out the derivation for the square of the magnetic field than for the absolute value, though - the behavior of the two functions in terms of stable points is the same. By the chain rule, we have:
\begin{equation} \nabla^2 B^2 = \sum_{i \in \left\{ x, y, z \right\} } 2\left| \nabla B_i \right|^2 + 2B_i\nabla^2 B_i. \end{equation}
By Maxwell’s equations, in free space $\nabla^2\vec{B} = \vec{0}$, which can only hold if each vector component ($\nabla^2 B_i$) is zero. Therefore:
\begin{equation} = \sum_{i \in \left\{ x, y, z \right\} } 2\left| \nabla B_i \right|^2 \geq 0. \end{equation}